看到这篇文章都斐波那契查找讲的很透彻,所以转载收藏一下。
斐波那契查找原理:
斐波那契查找是一种在有序表中高效查找指定元素的算法,比折半查找要复杂一些,主要复杂在要多做不少准备工作。下面看它的工作流程:
1.计算并保存一个斐波那契序列的数组,方便以后取值。数组名记为f,例如f[1]=1,f[2]=1,f[3]=2,f[4]=3,f[5]=5,f[6]=8,f[7]=13,f[8]=21
2.把有序数组的长度扩充到a.length=f[k]-1,k是满足条件的最小值,比如数组长度为13,那么就把它长度扩充到f[8]-1=20,所有在末尾添加的扩充元素都是原数组最后一个元素的复制品
3.找到mid元素,不断进行二分比较,直到找到目标元素为止,这一步的做法与折半查找一模一样,仅仅是计算mid的公式从(low+high)/2改为low+(f[k-1]-1)。
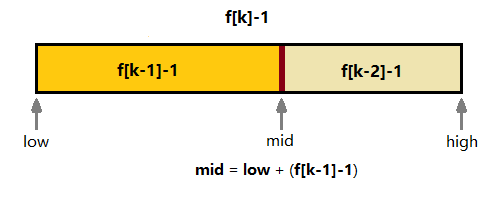
斐波那契查找的理解难点就一个:为什么需要把数组长度扩充到f[k]-1而不是f[k]或者f[k+1]?这是为了能正确递归计算mid值,看下图可发现 f[k]-1 = (f[k-1] + f[k-2]) - 1 = (f[k-1]-1) + 1 + (f[k-2]-1),中间的1就是我们二分的锚点mid,如果目标在左区,数组长度就缩到(f[k-1]-1),如果在右区,数组长度就缩到(f[k-2]-1),否则就等于mid完成查找。而(f[k-1]-1)又能拆成(f[k-2]-1)+1+(f[k-3]-1),这样递归分割下去就能不断的缩小区间直至找到目标。
斐波那契查找与折半查找的比较:
二者理论效率半斤八两,时间复杂度都是log2n,有人说斐波那契查找比折半查找效率高,理由有2个:1.斐波那契查找只用到加减法,而折半查找计算mid时要除以2,除法很影响效率;2.如果目标在low->mid区,只需要判断一次,而如果在mid->high需要判断2次(需要先判断不在low->mid区,再判断在mid->high区),斐波那契查找的low->mid区更大(0.618>0.5),有更多的概率只需要判断一次,所以总体判断次数更少。
原因1看起来有理,可是现在的编译器只要遇到/2操作,都会优化为>>1,位运算比加减法只快不慢,所以原因1不成立。原因2也貌似有些道理,可是如果按照这个道理推理下去,把分割点设在0.99岂不是更好?可0.99明显是个垃圾分割点,二分力度很差,所以这个理由我也不认可。
斐波那契查找的时间复杂度还是O(log 2 n ),但是 与折半查找相比,斐波那契查找的优点是它只涉及加法和减法运算,而不用除法,而除法比加减法要占用更多的时间,因此,斐波那契查找的运行时间理论上比折半查找小,但是还是得视具体情况而定。
对于斐波那契数列:1、1、2、3、5、8、13、21、34、55、89……(也可以从0开始),前后两个数字的比值随着数列的增加,越来越接近黄金比值0.618。比如这里的89,把它想象成整个有序表的元素个数,而89是由前面的两个斐波那契数34和55相加之后的和,也就是说把元素个数为89的有序表分成由前55个数据元素组成的前半段和由后34个数据元素组成的后半段,那么前半段元素个数和整个有序表长度的比值就接近黄金比值0.618,假如要查找的元素在前半段,那么继续按照斐波那契数列来看,55 = 34 + 21,所以继续把前半段分成前34个数据元素的前半段和后21个元素的后半段,继续查找,如此反复,直到查找成功或失败,这样就把斐波那契数列应用到查找算法中了。
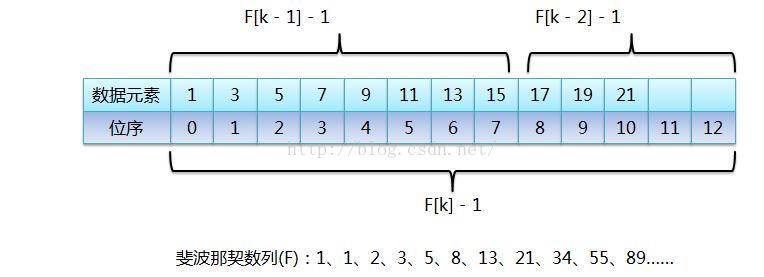
比如上面的表格中的数据元素为11,在斐波那契数列中是找不到,所以在末尾填充元素,例如在上述的位序中的11,12处添加21,21(重复的是末尾元素。)
代码实现:
/*@para:a[]:给定待查的数组,n为要查找的数组的个数,key:为要查找的关键字*/int Fibonacci_Search(int *a,int n,int key){ int low,high,mid,i,k=0; low=1; /* 定义最低下标为记录首位 */ high=n; /* 定义最高下标为记录末位 */ while(n>F[k]-1)//计算n位于斐波那契数列中的位置 k++; for (i=n;i<F[k]-1;i++)//将不满的数值补全 a[i]=a[n]; while(low<=high) { mid=low+F[k-1]-1; if (key<a[mid]) { high=mid-1; k=k-1; /*说明:low=mid+1说明待查找的元素在[low,mid-1]范围内,k-=1 说明范围[low,mid-1]内的 元素个数为F(k-1)-1个,所以可以递归的应用斐波那契查找*/ } else if (key>a[mid]) { low=mid+1; k=k-2;//说明:low=mid+1说明待查找的元素在[mid+1,hign]范围内,k-=2 说明范围 //[mid+1,high]内的元素个数为n-(F(k-1))= Fk-1-F(k-1)=Fk-F(k-1)-1=F(k- //2)-1个,所以可以递归的应用斐波那契查找 } else //前面两种情况都不满足,才会执行else { if (mid<=n) return mid; /* 若相等则说明mid即为查找到的位置 */ else return n; } } return 0;} 大部分说明都忽略了一个条件的说明:n=F(k)-1, 表中记录的个数为某个斐波那契数小1。这是为什么呢?
我想了很久,终于发现,原因其实很简单:
是为了格式上的统一,以方便递归或者循环程序的编写。表中的数据是F(k)-1个,使用mid值进行分割又用掉一个,那么剩下F(k)-2个。正好分给两个子序列,每个子序列的个数分别是F(k-1)-1与F(k-2)-1个,格式上与之前是统一的。不然的话,每个子序列的元素个数有可能是F(k-1),F(k-1)-1,F(k-2),F(k-2)-1个,写程序会非常麻烦